|
बी ए - एम ए >> बीए सेमेस्टर-5 पेपर-2 शिक्षाशास्त्र - शैक्षिक सांख्यिकी बीए सेमेस्टर-5 पेपर-2 शिक्षाशास्त्र - शैक्षिक सांख्यिकीसरल प्रश्नोत्तर समूह
|
5 पाठक हैं |
|||||||
बीए सेमेस्टर-5 पेपर-2 शिक्षाशास्त्र - शैक्षिक सांख्यिकी - सरल प्रश्नोत्तर
प्रश्न- दण्ड चित्र से आप क्या समझते हैं? ये कितने प्रकार के होते हैं इनका विस्तार पूर्वक वर्णन कीजिए।
उत्तर -
दण्ड-चित्र (Bar Diagrams) - दण्ड चित्र की रचना उस समय की जाती है जब ' अविछिन्न श्रेणी में व्यवस्थित आँकड़ों के केवल एक ही गुण का तुलनात्मक अध्ययन करना होता है। इनमें पद मूल्यों के साथ लम्बाई में दण्ड बनाये जाते हैं, जिनकी मोटाई समान होती है। मोटाई तथा दण्डों के मध्य सुविधानुसार स्थान लिये जाते हैं। ये चित्र व्यक्तिगत मूल्यों, काल श्रेणी एवं भौगोलिक श्रेणी आदि से सम्बन्धित आंकड़ों को प्रस्तुत करते हैं। इनका पद-मूल्यों से कोई विशेष सम्बन्ध नहीं होता है। ये विभिन्न प्रकार के होते हैं, जिन्हें कि निम्न चार्ट द्वारा समझा जा सकता है।
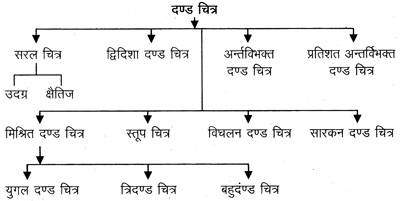
1. सरल दण्ड चित्र (Simple Bar Diagrams) - ये निम्नलिखित दो प्रकार के होते हैं-
(a) उदग्र दण्ड (Vertical Bars) - सीधे व खडे बनाये गये दण्ड उदग्र दण्ड कहलाते हैं। इन दण्डों को बनाते समय इस बात का पूर्ण प्रयत्न किया जाना चाहिए कि सबसे ऊँचा दण्ड बाएं और ऊँचाई के क्रम में अन्य दण्ड बनाते हुए सबसे छोटा दण्ड दायें बनाना चाहिए। जब समंक समय या किसी अन्य महत्वपूर्ण क्रम में दिये हों तब छोटे या बड़े का विचार किये बिना दण्ड उसी क्रम में बनाए रखने चाहिए। इस स्थिति में इनका क्रम विपरीत भी हो सकता है। इसे बनाते समय पैमाने का विशेष ध्यान रखना चाहिए।
(b) क्षैतिज दण्ड (Horizontal Bars) - सीधे अर्थात् लेटी हुई दशा में बनाए गये दण्ड क्षैतिज दण्ड कहलाते हैं। इन दण्डों को बनाते समय भी सबसे ऊपर बड़ा दण्ड और उससे छोटा दण्ड उसके नीचे और दण्डों को इसी क्रम में बनाते हुए सबसे छोटा दण्ड सबसे नीचे बनाया जाना चाहिए। लेकिन समंक समय या किसी अन्य महत्वपूर्ण क्रम में दिये होने की स्थिति में दण्ड उसी क्रम में बनाने चाहिए।
2. द्विदिशा दण्ड चित्र (Dialateral or Dua-directional Bar Diagrams) - इस चित्र को उस समय बनाया जाता है, जब दो विपरीत गुण वाले तथ्यों का प्रदर्शन किया जाता है। ये दण्ड आधार रेखा के दायें व बाएं बनाये जाते हैं। ये प्रत्येक स्थिति में शून्य रेखा को बीच में मानते हैं। इस प्रकार इन दण्डों को आधार रेखा के दोनों ओर दिखाया जाता है।
ये दण्ड चित्र दो विरोधी गुणों वाले तथ्यों को प्रदर्शित करने व उनकी तुलना करने में सहायक होते हैं। इस प्रकार ये दण्ड सुविधाजनक होते हैं।
3. अन्तर्विभक्त दण्ड चित्र (Sub-divided Bar Diagrams) -
इन दण्ड चित्रों का प्रयोग उस समय किया जाता है, जब एक ही राशि अनेक भांगों में विभाजित हो तो कुल राशि तथा उनके विभिन्न भागों को इन दण्डों द्वारा प्रदर्शित किया जा सकता है। ये दण्ड विभिन्न अंश कुल परिणाम के साथ अपना अनुपात प्रकट करते हैं और एक दूसरे के साथ तुलनीय होते है। इन दण्डों के द्वारा राशियों की तुलना तो होती ही है साथ ही साथ उनके विभिन्न अंगों की तुलना भी हो जाती है। इनके विभिन्न अंगों को विभिन्न चिन्हों या विभिन्न रंगों द्वारा प्रदर्शित किया जाता है। इन्हें बनाते समय पैमाने का विशेष ध्यान रखना चाहिए।
उदाहरण- अधिक उपज देने वाली फसलों के क्षेत्र को अन्तर्विभक्त दण्ड चित्र द्वारा प्रदर्शित कीजिए।
| वस्तु |
मिलियन हेक्टेयर 2001-02 |
2002-03 |
| गेहूँ | 6.5 | 10.0 |
| चावल | 6.0 | 7.5 |
| चना | 3.0 | 4.0 |
हल -
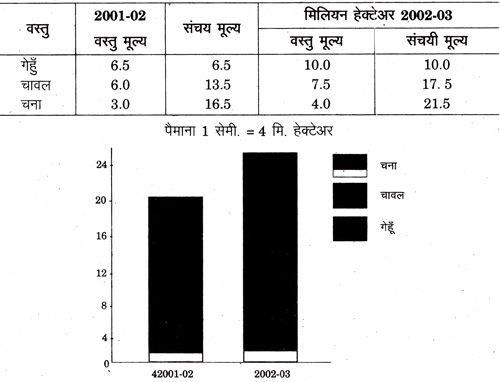
4. प्रतिशत अन्तर्विभक्त दण्ड-चित्र (Percentage Sub-divided Bar Diagrams) - इन दण्डों में पूर्ण मूल्य को 100 मानकर उसके विभिन्न भागों को प्रतिशत में प्रकट किया जाता है। इसमे सभी दण्ड 100 के बराबर होते हैं, जिनके कारण प्रत्येक दण्ड की लम्बाई व चौड़ाई बराबर होती है। केवल इसके अन्तर्विभाजन में प्रतिशत की भिन्नता के अनुसार अन्तर होता है। सामान्यतः ये चित्र आधार के एक ओर ही बनाये जाते हैं। लेकिन विपरीत सूचनाएँ दी हुई होने की स्थिति में इन्हें आधार के दोनों ओर भी बनाया जा सकता है। इन्हें पैमाने के आधार पर ही बनाया जाना चाहिए। ये दण्ड-चित्र अंशों की तुलना में सहायक होते है।
5. मिश्रित दण्ड-चित्र (Compound or Multiple Bar Diagrams) - समंकों के विभिन्न गुणों का तुलनात्मक चित्रण करना होता है तो इन दण्डों को पैमाने के आधार पर एक-दूसरे के साथ सटाकर बनाया जाता है। इन्हें समानता के अनुसार विभिन्न चिन्हों या रंगों द्वारा प्रदर्शित किया जा सकता है।
ये दण्ड-चित्र निम्नलिखित कई प्रकार के हो सकते हैं-
(a) युगल दण्ड-चित्र (Double Bar Diagrams)
(b) त्रिदण्ड चित्र (Treble Bar Diagrams)
(e) बहु-दण्ड चित्र (Multiple Bar Diagrams)
6. स्तूप-चित्र (Pyramid Diagram) - इस चित्र की आकृति स्तूप जैसी होने के कारण इसे स्तूप चित्र कहते हैं। इस चित्र का प्रयोग अधिकांशतः विभिन्न आयु के वर्गों के स्त्री-पुरुषों की संख्या को प्रदर्शित करने के लिए किया जाता है। इसमें आधार रेखा को बीच में उदग्र रूप में मानते हैं और उसके दोनों ओर क्षैतिज दण्ड की रचना एक-दूसरे से सटाकर की जाती है। इस चित्र के माध्यम से एक संख्या व शिक्षा सम्बन्धी आँकड़ों को आसानी से दिखाया जा सकता है। ये देखने में आकर्षक होते हैं। इनमें पैमाने को आधार मानना आवश्यक होता है।
7. विचलन दण्ड-चित्र (Deviation Bar Diagrams) - इन दण्ड चित्रों की रचना उस समय की जाती है, जब रचना, स्थान या समय के कारण समंकों में होने वाले परिवर्तन को प्रदर्शित करना होता है। इन चित्रों में मुख्य राशियों के शुद्ध विचलन को प्रदर्शित किया जाता है। इस चित्र के माध्यम से यह प्रदर्शित किया जाता है कि विचलन किस दिशा में व कितना है अर्थात् विचलन व उसकी दिशाओं का ज्ञान होता है। इन चित्रों को बनाते समय भी पैमाने को विशेष ध्यान में रखना चाहिए।
8. सरकन दण्ड-चित्र (Sliding Bar Diagrams) - ये दण्ड-चित्र द्विदिशा दण्ड-चित्र से मिलते-जुलते हुए होते हैं। इन्हें भी द्विदिशा दण्ड-चित्रों की भाँति ही बनाया जा सकता है, अन्तर केवल इतना है कि द्विदिशा दण्ड चित्रों की लम्बाई मूल्यों को प्रदर्शित करती है और इसीलिए सभी दण्डों की लम्बाइयाँ भिन्न-भिन्न होती हैं। इन दण्ड मूल्यों को 100 मानकर बनाया जाता है। जिसके कारण उनकी लम्बाई तो समान होती है किन्तु उनके विभागों की लम्बाई में भिन्नता पायी जाती है। इस प्रकार के दण्ड चित्रों को वहीं पर बनाया जाता है जहाँ पर मूल्य दो भागों में दिये हों और दोनों को प्रदर्शित किया जाना हो।
|
|||||
- प्रश्न- सांख्यिकी की परिभाषा दीजिए तथा इसकी प्रकृति और क्षेत्र की विवेचना कीजिए।
- प्रश्न- सांख्यिकी की प्रकृति की विवेचना कीजिए।
- प्रश्न- सांख्यिकी के प्रमुख कार्य क्या हैं?
- प्रश्न- सांख्यिकी के क्षेत्र की विवेचना कीजिए।
- प्रश्न- सांख्यिकी का महत्व स्पष्ट कीजिए।
- प्रश्न- सांख्यिकी की सीमाओं की विवेचना कीजिए।
- प्रश्न- सांख्यिकी के विभिन्न प्रकारों का विवरण प्रस्तुत कीजिए।
- प्रश्न- शिक्षा में सांख्यिकी का क्या महत्व है?
- प्रश्न- सांख्यिकी के उद्देश्यों की व्याख्या कीजिए।
- प्रश्न- सांख्यिकी के ऐतिहासिक पृष्ठभूमि की विवेचना कीजिए।
- प्रश्न- सांख्यिकी के प्रतीक पर प्रकाश डालिए।
- प्रश्न- निम्न अंकों से वर्गान्तरों की संख्या ज्ञात कीजिए एवं आवृत्तियां भी ज्ञात कीजिए।
- प्रश्न- दत्त और सांख्यिकी में क्या सम्बन्ध है? दत्तों के विभिन्न वर्गीकरण का विस्तार से उल्लेख कीजिए।
- प्रश्न- आवृत्ति बंटन से आपका क्या आशय है? इसके प्रकार व लाभ बताइए। आप किस प्रकार से खण्डित आवृत्ति बंटन करेंगे?
- प्रश्न- आवृत्ति वितरण के लाभ बताइए।
- प्रश्न- मूल प्रदत्तों को व्यवस्थित करने की विधियों पर प्रकाश डालिए।
- प्रश्न- 'चर' से आप क्या समझते हैं? इसके प्रकार बताइए।
- प्रश्न- संचयी बारम्बारता से आप क्या समझते हैं? इसके प्रकार समझाइये।
- प्रश्न- योग संचालन से आप क्या समझते हैं?
- प्रश्न- वर्ग सीमाओं के आधार पर वर्गान्तरों के निर्धारण की कौन-कौन सी विधियाँ हैं?
- प्रश्न- निम्न आँकड़ों से संचयी आवृत्ति सारणी बनाइये।
- प्रश्न- प्रदत्तों के आलेखीय चित्रण से आप क्या समझते हैं? शिक्षा में रेखाचित्रों के विभिन्न कार्यों का वर्णन कीजिए।
- प्रश्न- "रेखा का विचरण मस्तिष्क पर प्रभाव डालने वाले सारणित कथन की अपेक्षा अधिक शक्तिशाली होता है। यह उतनी शीघ्रता से, जितनी आँख कार्य करने की क्षमता रखती है, प्रकट करता है कि क्या हो रहा है और क्या होने वाला है।' वॉडिंगटन के इस कथन को स्पष्ट कीजिए।
- प्रश्न- दण्ड चित्र से आप क्या समझते हैं? ये कितने प्रकार के होते हैं इनका विस्तार पूर्वक वर्णन कीजिए।
- प्रश्न- आँकड़ों के रेखीय चित्रण के सामान्य सिद्धांत बताइए।
- प्रश्न- सांख्यिकी में रेखीय प्रदर्शन में प्रयुक्त वृत्त चित्र विधि का उदाहरण सहित वर्णन कीजिए।
- प्रश्न- निम्नलिखित सारणी का संचयी आवृत्ति वक्र चित्र बनाइये।
- प्रश्न- समंकों के बिन्दुरेखीय प्रदर्शन का महत्व बताइये। उसके विभिन्न लाभ एवं दोष क्या हैं?
- प्रश्न- समंकों के बिन्दुरेखीय प्रदर्शन के क्या लाभ हैं?
- प्रश्न- समंकों के बिन्दुरेखीय प्रदर्शन के क्या दोष हैं?
- प्रश्न- आवृत्ति वक्र से आप क्या समझते हैं?
- प्रश्न- बहुभुज एवं स्तम्भाकृति अंकित करने का तर्काधार दीजिए।
- प्रश्न- तोरण किसे कहते हैं?
- प्रश्न- स्तम्भाकृति का एक उदाहरण दीजिए।
- प्रश्न- बहुभुज किसे कहते हैं? समझाइए।
- प्रश्न- 50 अंकों की शिक्षाशास्त्र की एक परीक्षा में 40 छात्रों के प्राप्तांकों की आवृत्ति वितरण तालिका में नीचे दी गयी है। इन समंकों से आवृत्ति बहुभुज की रचना कीजिए।
- प्रश्न- आवृत्ति आयत चित्र पर टिप्पणी लिखिए।
- प्रश्न- निम्न समंकों को आवृत्ति आयत चित्र द्वारा प्रदर्शित कीजिए
- प्रश्न- निम्नलिखित आँकड़ों को त्रिदण्ड चित्र द्वारा प्रदर्शित कीजिए।
- प्रश्न- भारत में चीनी उत्पादन के निम्नलिखित समंकों को सरल दण्ड चित्र द्वारा प्रदर्शित कीजिए।
- प्रश्न- अग्रलिखित प्रमुख उत्पादन सम्बन्धी आँकड़ों को त्रिदण्ड चित्र द्वारा प्रदर्शित कीजिए।
- प्रश्न- मध्यमान से आप क्या समझते हैं? इसके महत्व एवं विधियों की व्याख्या कीजिए।
- प्रश्न- शिक्षा के क्षेत्र में मध्यमान का उपयोग एवं महत्व बताइये।
- प्रश्न- मध्यमान ज्ञात करने की प्रत्यक्ष विधि का उल्लेख उदाहरण सहित कीजिए।
- प्रश्न- मध्यमान ज्ञात करने की लम्बी विधि (Long Method) को उदाहरण सहित समझाइये।
- प्रश्न- मध्यमान् ज्ञात करने की सरल विधि उदाहरण सहित बताइये।
- प्रश्न- मध्यमान ज्ञात करने के लिए किन-किन बातों को ध्यान में रखना चाहिए?
- प्रश्न- बहुलांक से आप क्या समझते हैं? इसके महत्व एवं विधियों का उल्लेख कीजिए।
- प्रश्न- शिक्षा के क्षेत्र में बहुलांक की उपयोगिता स्पष्ट कीजिए।
- प्रश्न- बहुलांक ज्ञात करने की विधियों का उल्लेख कीजिए।
- प्रश्न- नीचे दिये गये आँकड़ों से मध्यमान एवं मध्यांक की गणना कीजिए :
- प्रश्न- मध्यांक से आप क्या समझते हैं? इसके महत्व एवं विधियों का उल्लेख कीजिए।
- प्रश्न- शिक्षा के क्षेत्र में मध्यांक के महत्व की विवेचना कीजिए।
- प्रश्न- मध्यांक ज्ञात करने की विधियों का उल्लेख कीजिए।
- प्रश्न- केन्द्रीय प्रवृत्ति के मापक कौन-कौन से हैं? इसकी परिभाषायें लिखिए।
- प्रश्न- केन्द्रीय प्रवृत्ति की मापों का उदाहरण सहित वर्णन कीजिए।
- प्रश्न- केन्द्रीय प्रवृत्ति के मानों के प्रयोग का संक्षिप्त वर्णन कीजिए।
- प्रश्न- सापेक्षिक स्थिति के मापों में प्रतिशतांक मान का वर्णन कीजिए।
- प्रश्न- मध्यमान एवं माध्यिका में अन्तर स्पष्ट कीजिए।
- प्रश्न- मध्यमान एवं बहुलक में अन्तर स्पष्ट कीजिए।
- प्रश्न- निम्नलिखित अव्यवस्थित समंकों से मध्यमान ज्ञात कीजिए -7, 10, 13, 15, 20
- प्रश्न- निम्नलिखित अव्यवस्थित संमकों से मध्यमान ज्ञात कीजिए - 7, 10, 8, 15, 9, 11
- प्रश्न- निम्नलिखित अव्यवस्थित संमकों से बहुलक ज्ञात कीजिए - 4, 6, 3, 4, 5, 7, 4, 8
- प्रश्न- निम्नलिखित अव्यवस्थित समंकों के मध्यमान ज्ञात कीजिए : 4, 6, 7, 5, 8, 6
- प्रश्न- निम्नलिखित अव्यवस्थित समंकों से माध्यिका ज्ञात कीजिए - 6, 8, 7, 10, 9, 12, 11
- प्रश्न- निम्नलिखित अव्यवस्थित समंकों से बहुलांक ज्ञात कीजिए : 3, 7, 4, 5, 3, 9, 3, 7, 3
- प्रश्न- निम्नलिखित का बहुलांक बताइये - 2, 2, 4, 6, 8, 10, 2, 5, 4, 2
- प्रश्न- केन्द्रीय प्रवृत्ति से क्या आशय है?
- प्रश्न- केन्द्रीय प्रवृत्ति की माप का अर्थ एवं परिभाषा स्पष्ट कीजिए।
- प्रश्न- निम्नलिखित का बहुलांक बताइये - 4, 6, 7, 5, 8, 6
- प्रश्न- मध्यांक का क्या अर्थ है? इसका प्रयोग कब करना चाहिए।
- प्रश्न- बहुलांक के क्या उपयोग हैं?
- प्रश्न- निम्न वितरण से समान्तर माध्य, मध्यका और बहुलक ज्ञात कीजिए।
- प्रश्न- (अ) निम्नलिखित आवृत्ति बंटन में यदि समान्तर माध्य का मान 18 हो तो अज्ञात आवृत्ति ज्ञात कीजिये?
- प्रश्न- निम्न समंकों से अज्ञात पद ज्ञात कीजिए।
- प्रश्न- निम्नलिखित संचयी आवृत्ति वितरण से समान्तर माध्य ज्ञात कीजिए :
- प्रश्न- निम्नलिखित समंकों से भूयिष्ठिक एवं मध्यिका ज्ञात कीजिए।
- प्रश्न- निम्नलिखित प्राप्तांकों का मध्यांक एवं बहुलांक ज्ञात कीजिए - 15, 23, 22, 17, 22, 18, 19, 22, 18, 24
- प्रश्न- निम्न सारणी को संशोधित कर मध्यका ज्ञात कीजिए -
- प्रश्न- निम्नलिखित अव्यवस्थित समंकों से बहुलांक ज्ञात कीजिए - 3, 7, 4, 2, 3, 9, 3
- प्रश्न- एक कक्षा के 20 विद्यार्थियों की आयु के समंक निम्नलिखित हैं। बहुलक ज्ञात कीजिए - 15, 17, 18, 20, 21, 22, 24, 15, 16, 17, 21, 22, 22, 23, 17, 22, 18, 22, 19, 20.
- प्रश्न- निम्नलिखित जूतों के आकार संख्या से भूयिष्ठिक ज्ञात कीजिए - जूतों की आकार की संख्या 3, 4, 2, 1, 7, 6, 6, 7, 5, 6, 8, 9, 5
- प्रश्न- निम्नलिखित आँकड़ों से बहुलक की गणना कीजिए.
- प्रश्न- निम्नलिखित सारणी से मध्यांक ज्ञात कीजिए -
- प्रश्न- निम्नलिखित सारणी से मध्यमान ज्ञात कीजिए :
- प्रश्न- निम्नलिखित सारिणी से मध्यांक ज्ञात कीजिए -
- प्रश्न- निम्नलिखित सारणी से मध्यमान ज्ञात कीजिए।
- प्रश्न- शतांशीय मान से आप क्या समझते हैं? इसके महत्व एवं विधियों का उल्लेख कीजिए।
- प्रश्न- शिक्षा के क्षेत्र में शतांशीय मान के उपयोग एवं महत्व को बताइये।
- प्रश्न- प्रतिशतांक क्रमांक का क्या अर्थ है? प्रतिशतांक व प्रतिशतांक क्रमांक में सम्बन्ध को समझाइये।
- प्रश्न- नीचे दिये गए व्यवस्थित प्राप्तांकों से यह ज्ञात करें कि उस विद्यार्थी का PR क्या होगा जिसका 15 और 41 प्राप्तांक है।
- प्रश्न- एम. ए. की 50 छात्राओं की कक्षा को परीक्षा में उपलब्धि पर क्रमांकित किया गया तथा उसमें पूजा को दूसरा स्थान प्राप्त हुआ तो उसका प्रतिशतांक क्रमांक क्या होगा?
- प्रश्न- यदि किसी विद्यार्थी का क्रमांक 5 है तो प्रतिशतांक क्रम क्या होगा?
- प्रश्न- विचलनशीलता के मापन से आप क्या समझते हैं? विचलनशीलता के मापन में प्रयुक्त विभिन्न विधियों की सूत्र संकेत सहित व्याख्या कीजिए।
- प्रश्न- विस्तार से आप क्या समझते हैं? इसको ज्ञात करने की विधियाँ बताइये।
- प्रश्न- प्रामाणिक विचलन से आप क्या समझते हैं? इसको ज्ञात करने की विधियाँ बताइये।
- प्रश्न- माध्य विचलन को परिभाषित कीजिए। ये किस प्रकार प्रमाप विचलन से भिन्न हैं?
- प्रश्न- माध्य विचलन और प्रमाप विचलन में अन्तर बताइए
- प्रश्न- प्रमाप विचलन से आप क्या समझते हैं? इसकी गणना कैसे की जाती है?
- प्रश्न- प्रमाप विचलन का महत्व स्पष्ट कीजिए।
- प्रश्न- अन्तर चतुर्थक विस्तार से आप क्या समझते हैं?
- प्रश्न- शतमक विस्तार से आप क्या समझते हैं?
- प्रश्न- शिक्षा के क्षेत्र में विचलन मापनों का क्या उपयोग होता है?
- प्रश्न- विचलन की विभिन्न मापों की विशेषताओं की तुलना कीजिए।
- प्रश्न- धनात्मक तथा ऋणात्मक वैषम्यताओं की तुलना चित्र खींचकर कीजिए।
- प्रश्न- मानक विचलन के उपयोग बताइये।
- प्रश्न- विस्तार का क्या अर्थ है?
- प्रश्न- विस्तार के गुण बताइये।
- प्रश्न- विस्तार के दोष बताइये।
- प्रश्न- दिये गये अंकों से माध्य विचलन गुणांक की गणना कीजिए। 22, 25, 20, 18, 16, 21, 29, 26, 19, 24
- प्रश्न- प्राप्तांकों के निम्नलिखित वितरण के लिए मानक विचलन तथा चतुर्थक विचलन की गणना कीजिए।
- प्रश्न- प्राप्तांकों के निम्नलिखित वितरण के लिए मानक विचलन तथा चतुर्थक विचलन की गणना कीजिए।
- प्रश्न- मानक विचलन क्या है? प्राप्तांकों के निम्नलिखित वितरण के लिये मानक विचलन की गणना कीजिए -
- प्रश्न- मानक विचलन क्या है? प्राप्तांकों के निम्नलिखित वितरण के लिए मध्यमान तथा मानक विचलन की गणना कीजिए
- प्रश्न- मानक विचलन से आप क्या समझते हैं? निम्नलिखित आवृत्ति वितरण से संक्षिप्त विधि द्वारा मानक विचलन की गणना कीजिए
- प्रश्न- प्रसार एवं शतमक से आप क्या समझते हैं? निम्नलिखित अंकों का चतुर्थांक विचलन (Q.D.) ज्ञात कीजिए : 31, 30, 22, 27, 32, 17, 26, 34, 21, 24, 19
- प्रश्न- सह-सम्बन्ध से आप क्या समझते हैं? शिक्षा के क्षेत्र में इसका उपयोग कब किया जाता है?
- प्रश्न- शिक्षा के क्षेत्र में सह-सम्बन्ध का उपयोग कब किया जाता है?
- प्रश्न- दो चर श्रेणियों के मध्य सह-सम्बन्ध की गणना के लिए संगामी विचलन रीति को उदाहरण सहित समझाइये।
- प्रश्न- सह-सम्बन्ध से आप क्या समझते हैं? सह-सम्बन्ध के प्रकार तथा विभिन्न विधियाँ का उल्लेख कीजिये।
- प्रश्न- सह-सम्बन्ध का क्या अर्थ है? सहसम्बन्ध के प्रकार व उपयोगिता का वर्णन कीजिए।
- प्रश्न- कोटि अन्तर सह-सम्बन्ध की गणना करने के लिये किसके द्वारा निर्मित सूत्र का प्रयोग किया जाता है? सूत्र भी लिखिये।
- प्रश्न- सह-सम्बन्ध ज्ञात करते समय किन-किन बातों को ध्यान में रखना आवश्यक है?
- प्रश्न- सम्भाव्य विभ्रम तथा प्रमाप विभ्रम में अन्तर स्पष्ट कीजिए।
- प्रश्न- धनात्मक व ऋणात्मक सह-सम्बन्ध में अन्तर स्पष्ट कीजिए।
- प्रश्न- सह-सम्बन्ध से आप क्या समझते हैं? स्पीयरमैन सहसम्बन्ध गुणांक का सूत्र बताइये और उसमें प्रयुक्त संकेताक्षरों की व्याख्या कीजिए।
- प्रश्न- सह-सम्बन्ध गुणांक की परिभाषा बताइये। इसके गुणों का उल्लेख कीजिए।
- प्रश्न- सह-सम्बन्ध कितने प्रकार का होता है? निम्नांकित अंकों के आधार पर स्पीयरमैन की कोटि अन्तर विधि से सह-सम्बन्ध ज्ञात कीजिए।
- प्रश्न- सह-सम्बन्ध से आप क्या समझते हैं? निम्नांकित अंकों के आधार पर स्पीयरमैन को कोटि अन्तर विधि से सहसम्बन्ध ज्ञात कीजिए।
- प्रश्न- निम्नलिखित दस विद्यार्थियों के विज्ञान और गणित में प्राप्तांक दिये गये हैं। पियर्सन सहसम्बन्ध गुणांक निकालिए :
- प्रश्न- निम्नांकित अंकों के आधार पर कोटि अन्तर विधि से सहसम्बन्ध गुणांक ज्ञात कीजिए :
- प्रश्न- निम्नांकित अंकों के आधार पर कोटि अन्तर विधि से सहसम्बन्ध गुणांक ज्ञात कीजिए।
- प्रश्न- निम्नांकित अंकों के आधार पर स्पीयर मैन की कोटि अंतर विधि से सह-सम्बन्ध ज्ञात कीजिए।
- प्रश्न- अग्रलिखित आँकड़ों से कोटि अन्तर विधि द्वारा सहसम्बन्ध गुणांक की गणना कीजिए :
- प्रश्न- निम्न अंकों के आधार पर कोटि अन्तर विधि से सह-सम्बन्ध गुणांक की गणना कीजिए।
- प्रश्न- सामान्य सम्भावना वक्र क्या है? तथा इसमें कौन-सी विशेषताएँ पायी जाती हैं?
- प्रश्न- सामान्य प्रायिकता वक्र में कौन-कौन सी विशेषताएँ पायी जाती है?
- प्रश्न- सामान्य संभावना वक्र से क्या समझते हैं? इसके स्वरूप का वर्णन कीजिए।
- प्रश्न- सामान्य प्रायिकता वक्र के क्या उपयोग है?














